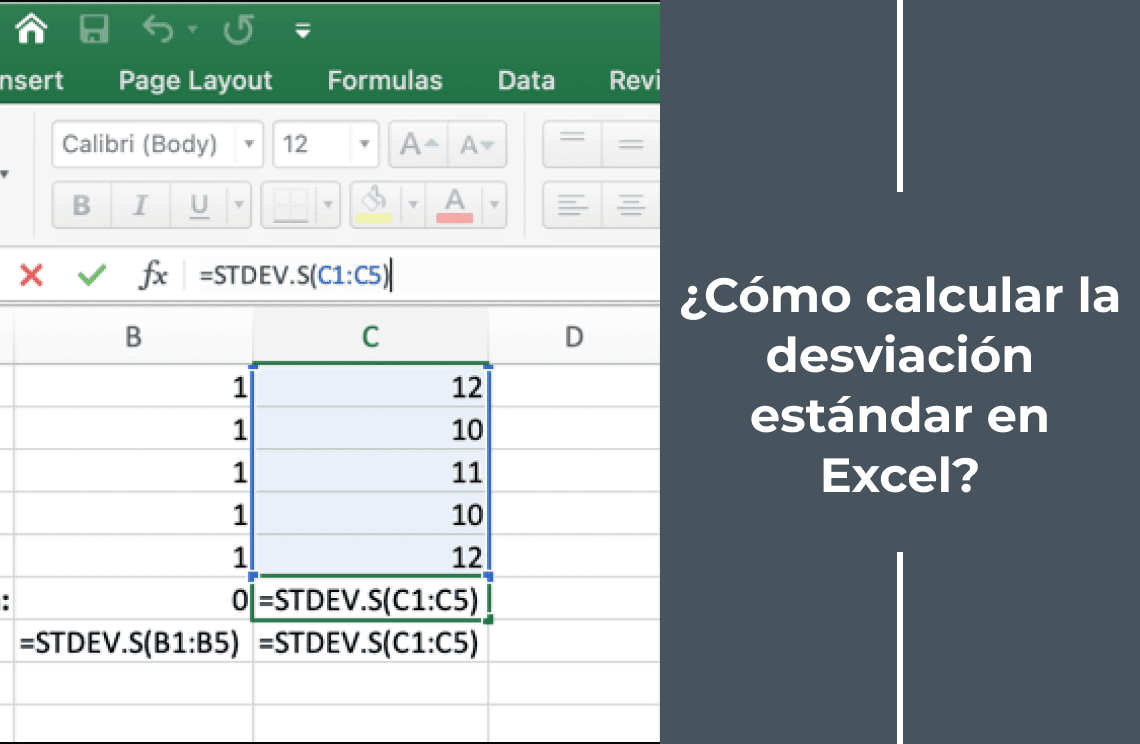
Procedimiento rápido! Ingrese sus datos en un rango seleccionado de celdas para encontrar la desviación estándar en Excel. Ahora, use =STDEV.S() si sus datos representan una muestra o =STDEV.P() si representan una población. ¡Eso es todo!
¿Qué es la desviación estándar?
Simplemente, la desviación estándar mide la dispersión de sus puntos de datos con respecto al análisis promedio. Responde a la pregunta: «¿Mis valores son consistentes o altamente variables?» Ejemplo:
Baja desviación estándar:
Estudiar 5, 6, 5, 6 y 5 horas semanales muestra números cercanos al promedio, lo que indica consistencia y una baja desviación estándar.
Alta desviación estándar
El rango de tiempo de estudio de 3, 9, 2, 12 y 5 horas semanales indica alta variabilidad y desviación estándar.
¿Qué es la desviación estándar en Excel?
La desviación estándar en Excel mide la dispersión de los datos alrededor de la media. Cuantifica la variación o dispersión de los valores del conjunto de datos. Use =STDEV.S para datos de muestra y =STDEV.P para datos de población. Ayuda a analizar cómo difieren los puntos de datos del promedio.
Solución rápida: ¿Cómo calcular la desviación estándar en Excel?
Primero, ingrese sus datos en Excel y use STDEV.P() para poblaciones o STDEV.S() para muestras. Sin embargo, STDEV.P() divide por el número total de puntos de datos y STDEV.S() divide por n-1 para la variabilidad de la muestra.
Entonces, si sus datos están en las celdas B2 a B31, use =STDEV.P(B2:B31) para la población o =STDEV.S(B2:B31) para la muestra. Excel calculará la desviación estándar.
Aplicaciones del mundo real de la desviación estándar
- Control de calidad: Mide la consistencia de los productos en la fabricación.
- Finanzas: Evalúa la volatilidad y el riesgo de las inversiones.
- Educación: Evalúa la dispersión de las calificaciones de los estudiantes.
- Pronóstico del clima: Analiza la variabilidad en los datos de temperatura o precipitaciones.
- Atención médica: Monitorea la variación en los tiempos de recuperación de los pacientes.
- Investigación de mercado: Evalúa la dispersión de las preferencias de los consumidores en las encuestas.
- Análisis de rendimiento: Evalúa la consistencia del rendimiento de los atletas.
Tipos de desviación estándar
- Desviación estándar de la población: Mide la dispersión de los datos para una población completa.
- Desviación estándar de la muestra: Estima la dispersión de los datos dentro de una muestra, utilizando (n - 1) (corrección de Bessel) en el cálculo.
Diferencia entre
|
|
Fórmulas de desviación estándar
La fórmula de la desviación estándar de la población (σ) es:
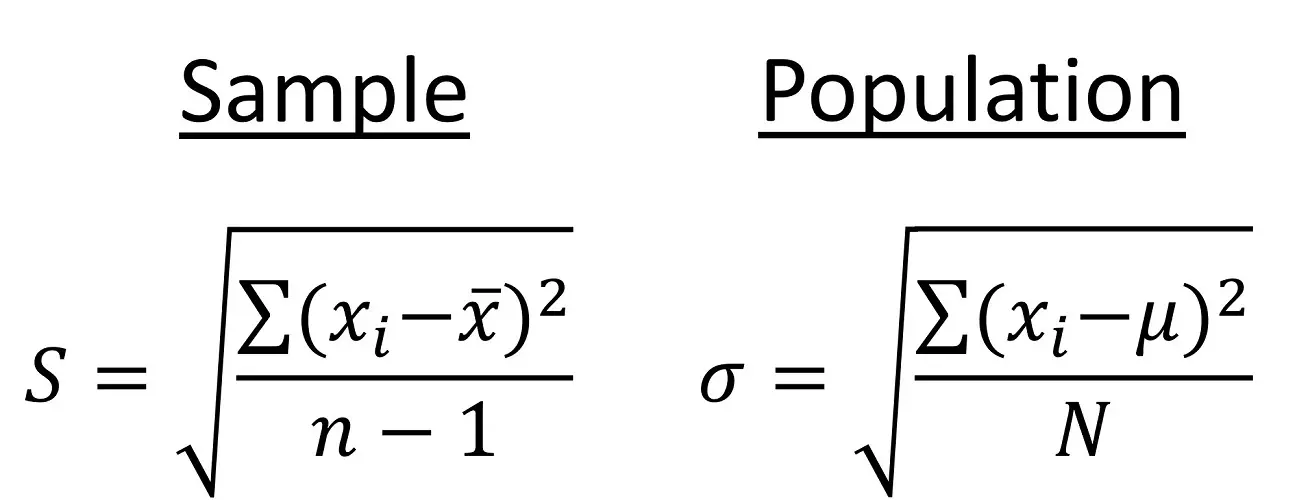
Aquí:
- N es el número total de puntos de datos en la población.
- xᵢ representa cada punto de datos individual.
- μ es la media de la población (promedio).
La fórmula determina el promedio de las desviaciones cuadradas de la media y luego calcula la raíz cuadrada de este promedio.
Fórmula de la desviación estándar de la muestra (s):
Aquí usamos n en minúscula por convención.
Aquí:
- n es el número de puntos de datos en la muestra.
- xᵢ es cada punto de datos individual.
- x̄ es la media de la muestra (promedio).
Esta fórmula usa (n - 1) (corrección de Bessel) para asegurar que la desviación estándar de la muestra estime sin sesgo la desviación estándar de la población.
¿Por qué STDEV.S es más común?
STDEV.S es más común porque generalmente trabajamos con una muestra de datos, no con toda la población. Dado que los conjuntos de datos completos son raros, STDEV.S es la opción preferida.
¿Cómo calcular la desviación estándar en Excel?
1. Ingrese sus datos de ventas: Abra Excel y coloque el número de ventas de cada día en una sola columna, por ejemplo, desde la celda B2 hasta B31.
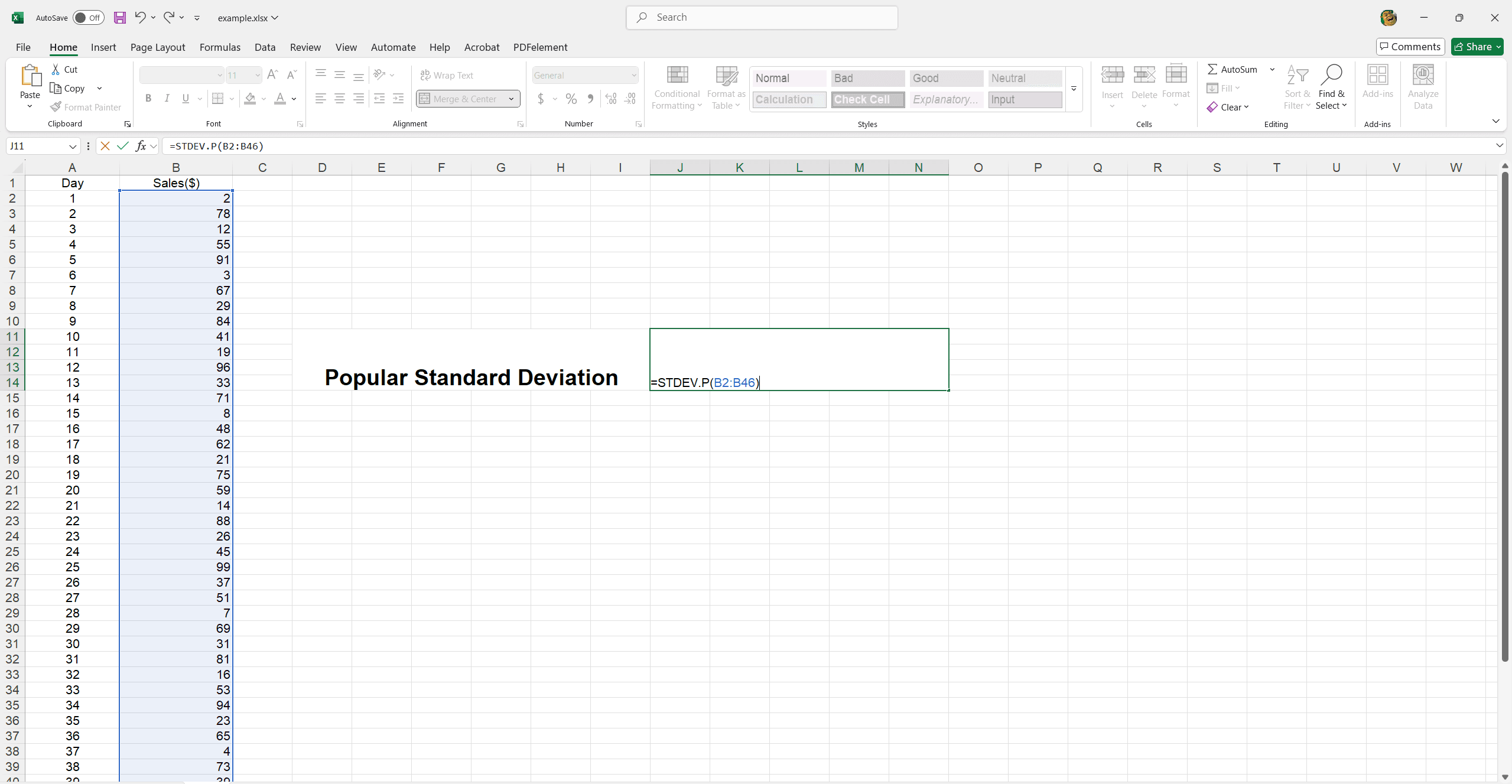
2. Calcular la desviación estándar de la población (si tiene TODOS los datos):
Vaya a una celda vacía (como E6). Escriba esta fórmula: =STDEV.P(B2:B31) y presione Enter. Este número le indica cuánto difieren sus ventas diarias del promedio de ventas diarias para el mes completo.
3. Calcular la desviación estándar de la muestra (si sus datos son solo una INSTANTÁNEA):
Si sus 30 días de datos son solo una muestra de un período más largo (como intentar adivinar la variación de todo un año), vaya a otra celda vacía. Escriba esta fórmula: =STDEV.S(B2:B31) y presione Enter.
Esto le da una estimación de la variación de ventas que podría ver en un período más largo. Comprender el resultado: el número de desviación estándar le indica qué tan dispersas están sus ventas diarias.
4. Un número pequeño significa que sus ventas diarias son bastante consistentes.
5. Un número grande significa que sus ventas diarias varían mucho.
¿Cómo interpretar los valores de desviación estándar?
Para interpretar mejor la desviación estándar, también podemos calcular la media de nuestros datos de ventas utilizando la siguiente ecuación.
En la celda E7, el valor medio se calcula en $975, como se ilustra a continuación.
¿Cómo agregar barras de desviación estándar en Excel?
Integrar barras de desviación estándar en nuestros gráficos de Excel proporciona una representación visual clara de la variabilidad de los datos.
1. Resalte el rango de datos de B2 a B31 en su ejemplo.
2. Vaya a la pestaña Insertar.
3. Elija su tipo de gráfico preferido (por ejemplo, gráfico de líneas) como se ilustra en la imagen a continuación.
4. Inserte el gráfico.
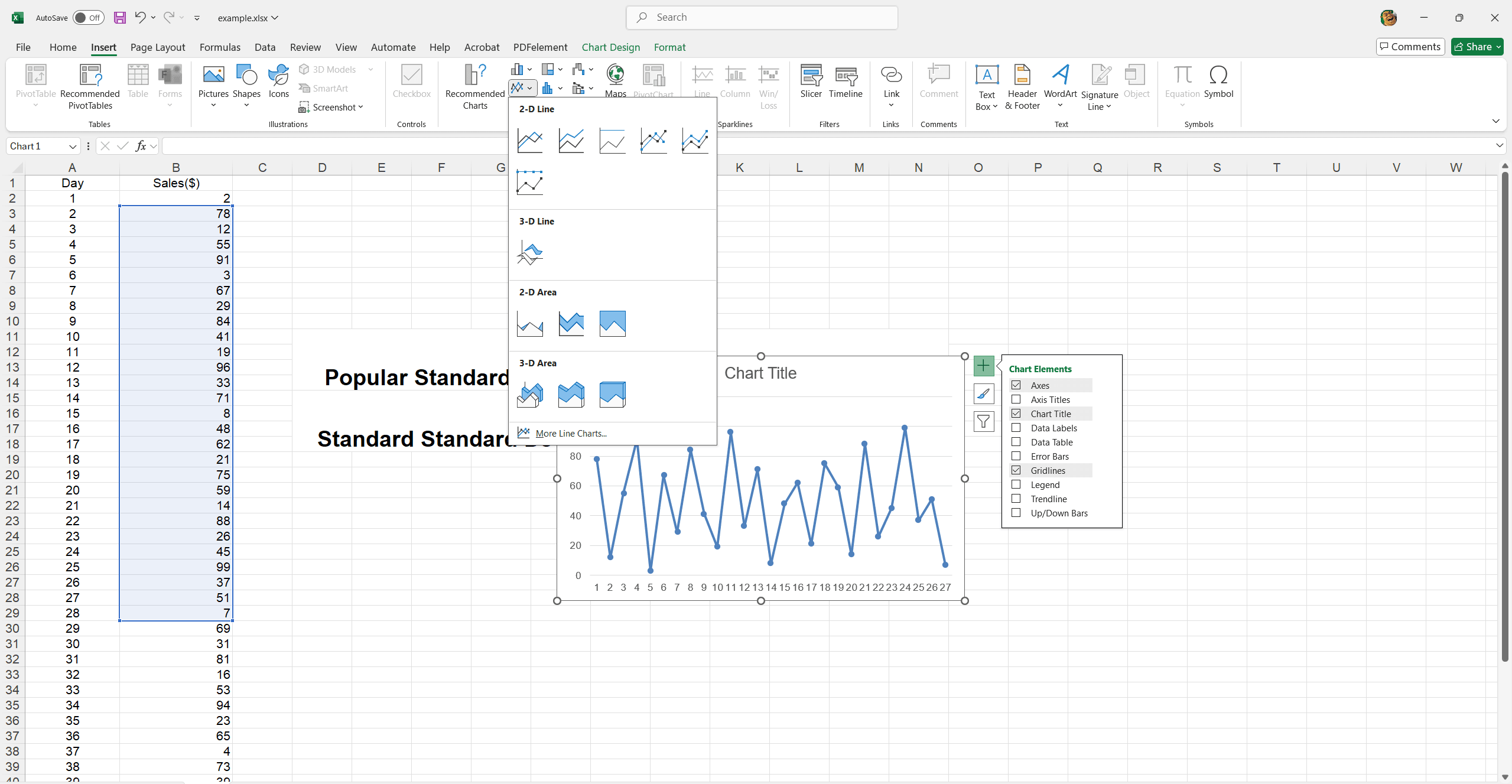
Aparecerá un gráfico de líneas básico a continuación.
1. Resalte su serie de datos en el gráfico. Vaya a la pestaña Diseño de gráfico.
2. Haga clic en Agregar elemento de gráfico en el grupo Diseños de gráfico.
3. Mueva el cursor sobre Barras de error.
4. Elija Desviación estándar para incluir barras de desviación estándar en el gráfico de líneas.
5. Pase el cursor sobre Barras de error y haga clic en Más opciones de barras de error para ajustar el color, el ancho y el estilo.
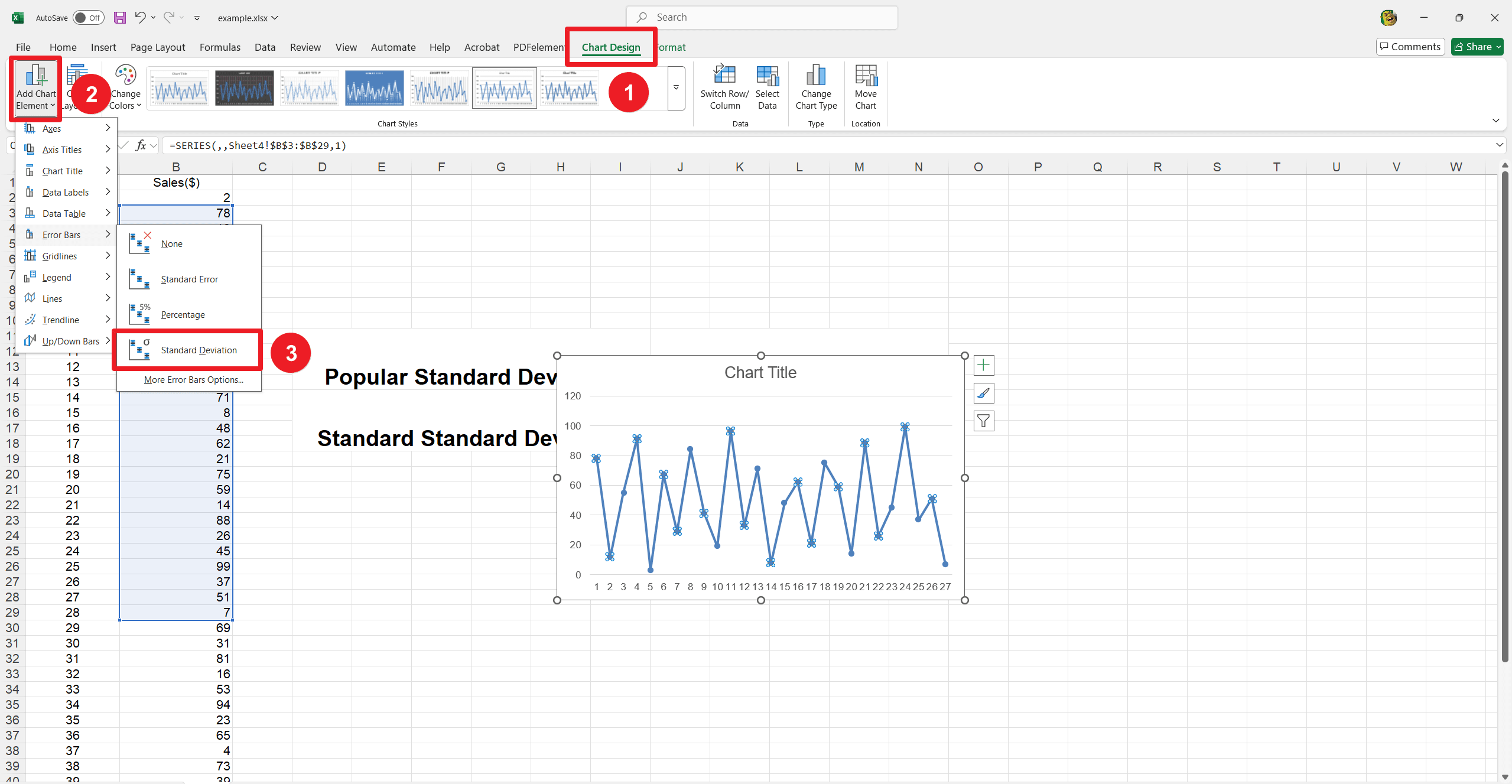
6. Ajuste estos parámetros en el panel Formato de barras de error hasta obtener el aspecto deseado.
Reflexiones finales
Comprender y utilizar la desviación estándar, especialmente STDEV.S, puede cambiar la forma en que ve sus datos. Ya sea que esté rastreando horas de estudio o métricas comerciales, dominar la consistencia frente a la variabilidad es útil. Así que, la próxima vez que se sumerja en sus números, recuerde que un poco de conocimiento estadístico puede marcar la diferencia. ¡Feliz análisis de datos!
Y si tiene hambre de más consejos de Excel o simplemente está curioso por descubrir nuevos trucos para mejorar sus habilidades, no olvide consultar algunos recursos fantásticos en PDF Agile. ¡Tienen excelentes consejos de Excel y guías prácticas que pueden llevar su análisis de datos al siguiente nivel!